Category: MiWORD of the Day

Look! You’ve finally made it to Canada! You gloriously take in the view of Lake Ontario when your friend beside you exclaims, “Look, they have beaver tails!” You excitedly scan the lake, asking, “Where?” 

“There!”

“Where?”

“There!”

You see no movement from the lake. It isn’t until your friend pulls you to the front of a storefront says “BeaverTails” with a picture of delicious pastries that you realize they didn’t mean actual beavers’ tails. It turns out you were looking at the wrong place the whole time!

Often times, it’s easy for us to quickly identify objects because we know the context of where things should be. These are the kinds of things we take for granted, until it’s time to hand the same tasks over to machines. 

In medical imaging, experts label what are called Regions of Interests (ROIs), which are specific areas of a medical image that contain pathology, such as the specific area of a lesion. Having labelled ROIs are important, as it can help prevent extra time from being wasted on analyzing non-relevant areas of an image, especially since medical images contain complex structures that take time to interpret. But in the area of machine learning (ML) in medical imaging, having labelled ROIs is also useful because it can help with training ML models that classify whether a medical image contains a pathology or not; with ROIs identified, cropping can be done during the preprocessing of images so that only relevant areas of images are compared for the model to learn differences between positive and negative images faster.

In fact, having ROIs is so important, there is an entire field in artificial intelligence dedicated to it: Computer Vision. The field of computer vision focuses on automating the extraction of ROIs in images or videos, which plays a critical role in the mechanization of tasks like object detection and tracking for things like self-driving cars. In object detection, for example, things like ROI Pooling can be utilized; this is where multiple ROIs are used to obtain input feature maps, from which maximum values are used to detect the presence of features, giving rise to the ability to identify many objects at once – this is extremely useful, especially once you’re on the road and there are 10 other cars around you!

Now, the fun part: using Region of Interest in a sentence!

Serious: The coordinates of ROIs are given for the positive mammogram images in the dataset I’m using. Maybe I could use Grad-CAM to see if the ML breast cancer classification model I’m using uses the same regions of the image to arrive at its classification decision; this way, I can see if its decision making aligns with the decision making of radiologists.

Less serious: I forced my friend to watch my favorite movie with me, but I can’t lie – I think the attractive male lead was her only region of interest!

See you in the blogosphere,

Yan Qing Lee

According to the dictionary, the term “adversarial” refers to a situation where two parties or sides oppose each other. But what about the “adversarial example”? Does it imply an example of two opposing sides? In a way, yes.

In machine learning, an example is one instance of the dataset. Adversarial examples are examples with calculated and imperceptible perturbation that tricks the model into the wrong prediction but look the same to humans. So “adversarial”, in this case, indicates opposition between something (or human) and the model. The adversarial examples are intentionally crafted to trick the model by exploiting its vulnerabilities.

How it works? There are many ways to find weak spots and generate adversarial examples, but FGSM is one classic way, and the goal is to make small changes to a picture such that it outputs the wrong prediction. First, we input the model with the picture. Assume the model outputs the correct prediction, so the loss function, which represents the difference between the prediction and the true label, will be low. Second, we compute the gradient of the loss function to tell us whether we should add or subtract a certain value epsilon to each pixel to make the loss bigger. Epsilon is typically very small, resulting in a tiny change to the value. Now, we have a picture that looks the same as the original but will trick the model into the opposite prediction!

One exciting property of adversarial examples is their transferability. It is known that adversarial examples created for one model can also trick other unknown models. This might be due to inherent flaws in the pattern recognition mechanisms of all models and, sometimes, model similarities, allowing these adversarial examples to exploit common vulnerabilities and lead to incorrect predictions.

Now, use “adversarial example” in a sentence by the end of the day: 

Kinda Serious: “Oh I can’t believe my eyes. I am seeing a dog right here and the model says it’s a cupcake…So you’re saying it might be an adversarial image? What even is that? The model is just dumb.”

Less Serious: Apparently, the movie star has an adversarial relationship with the media, but which stars have a good relationship with the media nowadays?

See you in the blogosphere,

Yuxi Zhu

Imagine you’re trying to compare two images—not just any images, but complex medical images like MRIs or X-rays. You want to know how similar they are, but traditional methods like simply comparing pixel values don’t always capture the whole picture. This is where Learned Perceptual Image Patch Similarity, or LPIPS, comes into play.

Learned Perceptual Image Patch Similarity (LPIPS) is a cutting-edge metric for evaluating perceptual similarity between images. Unlike traditional methods like Structural Similarity Index (SSIM) or Peak Signal-to-Noise Ratio (PSNR), which rely on pixel-level analysis, LPIPS utilizes deep learning. It compares images by passing them through a pre-trained convolutional neural network (CNN) and analyzing the features extracted from various layers. This approach allows LPIPS to capture complex visual differences more closely aligned with human perception. It is especially useful in applications such as evaluating generative models, image restoration, and other tasks where perceptual accuracy is critical.

Why is this important? In medical imaging, where subtle differences can be crucial for diagnosis, LPIPS provides a more accurate assessment of image quality, especially when images have undergone various types of degradation, such as noise, blurring, or compression.

Now, let’s use LPIPS in sentences!

Serious: When evaluating the effectiveness of a new medical imaging technique, LPIPS was used to compare the generated images to the original scans, showing that it was more sensitive to perceptual differences than traditional metrics.

Less Serious: I used LPIPS to compare my childhood photos with recent ones. According to the metric, I’ve definitely “degraded” over time!

See you in the blogosphere!

Jingwen (Lisa) Zhong

Volumetric rendering stands at the forefront of visual simulation technology. It intricately models how light interacts with myriad tiny particles to produce stunningly realistic visual effects such as smoke, fog, fire, and other atmospheric phenomena. This technique diverges significantly from traditional rendering methods that predominantly utilize geometric shapes (such as polygons in 3D models). Instead, volumetric rendering approaches these phenomena as if they are composed of an immense number of particles. Each particle within this cloud-like structure has the capability to absorb, scatter, and emit light, contributing to the overall visual realism of the scene. 

This is not solely useful for generating lifelike visual effects in movies and video games; it also serves an essential function in various scientific domains. Volumetric rendering enables the visualization of intricate three-dimensional data crucial for applications such as medical imaging, where it helps in the detailed analysis of body scans, and in fluid dynamics simulations, where it assists in studying the behavior of gases and liquids in motion. This technology, thus, bridges the gap between digital imagery and realistic visual representation, enhancing both our understanding and our ability to depict complex phenomena in a more intuitive and visually engaging manner. 

How does this work? 

Let’s start by talking about direct volume rendering. Instead of trying to create a surface for every object, this technique directly translates data (like a 3D array of samples, representing our volumetric space) into images. Each point in the volume, or voxel , contains data that dictates how it should appear based on how it interacts with light. 

For example, when visualizing a CT scan, certain data points might represent bone, while others might signify soft tissue. By applying a transfer function—a kind of filter—different values are mapped to specific colors and opacities. This way, bones might be made to appear white and opaque, while softer tissues might be semi-transparent. 

The real trick lies in the sampling process. The renderer calculates how light accumulates along lines of sight through the volume, adding up the contributions of each voxel along the way. It’s a complex ballet of light and matter, with the final image emerging from the cumulative effect of thousands, if not millions, of tiny interactions. 

Let us make this a bit more concrete. We first have transfer functions, a transfer function maps raw data values to visual properties like color and opacity. Let us represent the color assigned to some voxel as C(v) and the opacity as α(v). For each pixel in the final image, a ray is cast through the data volume from the viewer’s perspective. For this we have a ray equation: 

Where P(t) is a point along the ray at parameter 𝑡, P₀ is the ray’s origin, and is the normalized direction vector of the ray. As the ray passes through the volume, the renderer calculates the accumulated color and opacity along the ray. This is often done using compositing, where the color and opacity from each sampled voxel are accumulated to form the final pixel color. 

You probably used Volumetric Rendering 

Volumetric rendering transforms CT and MRI scans into detailed 3D models, enabling doctors to examine the anatomy and functions of organs in a non-invasive manner. A specific application includes most of the modern CT viewers. Volumetric rendering is key in creating realistic simulations and environments. In most AR applications, it is used under the hood to overlay interactive, three-dimensional images on the user’s view of the real world, such as in educational tools that project anatomical models for medical students. 

Now for the fun part (see the rules here), using volume rendering  in a sentence by the end of the day: 

Serious: The breakthrough in volumetric rendering technology has enabled scientists to create highly detailed 3D models of the human brain. 

Less Serious: I tried to use volumetric rendering to visualize my Netflix binge-watching habits, but all I got was a 3D model of a couch with a never-ending stream of pizza and snacks orbiting around it. 

…I’ll see you in the blogosphere. 

You might be thinking, “KL Divergence? Sounds exotic. Is it something to do with the Malaysian capital (Kuala Lumpur) or a measurement (kiloliter)?” Nope, and nope again! It stands for Kullback-Leibler Divergence, a fancy name for a metric to compare two probability distributions.

But why not just compare their means? After all, who needs these hard-to-pronounce names? Kullback… What was it again? That’s a good point! Here’s the catch: two distributions can have the same mean but look completely
different. Imagine two Gaussian distributions, both centered at zero, but one is wide and flat, while the other is narrow and tall. Clearly, not similar!

So, maybe comparing the mean and variance would work? Excellent thinking! But what if the distributions aren’t both Gaussian? For example, a wide and flat Gaussian and a uniform distribution (totally flat) might look similar visually, but the uniform distribution is not parametrized by a mean or variance. So, what do we compare?

Enter KL Divergence!

KL Divergence returns a single number that tells us how similar two distributions are, regardless of their types. The smaller the number, the more similar the distributions. But how do we calculate it? Here’s the formula (don’t worry, you don’t have to memorize it!).

Notice, if the distribution q has probability mass where p doesn’t, the KL Divergence will be large. Good, that’s what we want! But, if q has little mass where p has a lot, the KL Divergence will be small. Wait, that’s not what we want! No, it’s not, but luckily KL Divergence is asymmetric! KL(q || p) returns a different value than KL(p || q), so
we can compute both! Why are they different? I’ll leave that up to you to figure out!

KL Divergence in Action

Now, the fun part: using KL Divergence in a sentence!

Serious: Professor, can we approximate one distribution with another by minimizing the KL Divergence between them? That’s a great question! You’ve just stumbled on the idea behind Variational Inference.

Less Serious: Ladies and gentlemen, the KL Divergence between London and Kuala Lumpur is large, and so our flight time today will be 7 hour and 30 minutes. Please remember to stow your hand luggage in the overhead bins above you, fold your tray tables, and fasten your seatbelts.

See you in the blogosphere,
Benedek Balla

Have you ever tried to assemble a Lego set and ended up with mysterious extra pieces? Or perhaps you have cleaned up after a big party and found some confetti hiding in the corners days later? Welcome to the world of “residuals”!

Residuals pop up everywhere. It’s an everyday term but it’s actually fancier than just referring to the leftovers of a meal; it’s also a term used in regression models to describe the difference between observed and predicted values, or in finance to talk about what’s left of an asset. However, nothing I mentioned compares to the role residuals played in machine learning and particularly training deep neural networks.

When you learn an approximation of a function from an input space to an output space using backpropagation, the weights are updated based on the learning rate and gradients that are calculated through chain rule. As a neural network gets deeper, you have to multiply a small value—usually much smaller than 1—multiple times to pass it to the earliest layers, making the neural network excessively hard to optimize. This phenomenon prevalent in deep learning is call the vanishing gradient problem.

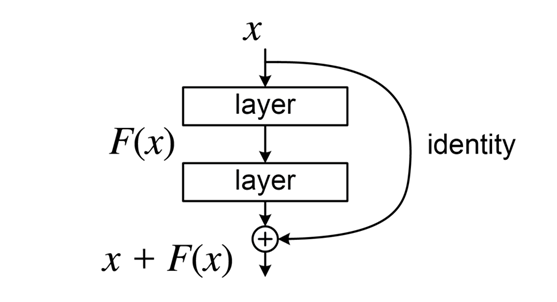
However, notice how deep layers of a neural network are usually composed by mappings that are close to identity. This is exactly why residual connections do their magic! Suppose your true mapping from input to output is h(x), and let the forward pass be f(x)+x. It follows that the mapping subject to learning would be h(x)-x, which is close to a zero function. This means f(x) would be way easier to learn under the vanishing gradient problem, since functions that are close to zero functions demand a lower level of sensitivity to each parameter, unlike the identity function.

Now before we dive too deep into the wizardry of residuals, should we use residual in a sentence?

Serious: Neuroscientists wanted to explore if CNNs perform similarly to the human brain in visual tasks, and to this end, they simulated the grasp planning using a computational model called the generative residual convolutional neural network.

Less serious: Mom: “What happened?”
Me: “Sorry Mom, but after my attempt to bake chocolate cookies, the residuals were a smoke-filled kitchen and a cookie-shaped piece of charcoal that even the dog wouldn’t eat”

See you in the blogosphere,
Mason Hu

Silhouette score… is that some sort of way to measure whose silhouette looks better? Or how identifiable the silhouettes are? Well… kind of! It turns out that in statistics, silhouette score is a measure for how “good” a clustering algorithm is. It considers two factors: cohesion and separation. Particularly, how compact is the cluster? And how separated is the cluster from other clusters?

Let’s say you asked your friend to group a bunch of cats into 3 clusters based on where they were sitting on the floor, because you wanted to know whether the cats sit in groups or if they just sit randomly. How can we determine how “good” your friend clustered them? Let’s zoom in to one specific cat who happens to be placed in Cluster 1. We first look at intra-cluster distance, which would be the mean distance to all other cats in Cluster 1. We then take the mean nearest-cluster distance, which would be the distance between the cat and the nearest cluster the cat is not a part of, either Cluster 2 or 3, in this case.

To have a “good” clustering algorithm, we want to minimize the intra-cluster distance and maximize the mean nearest-cluster distance. Together, this can be used to calculate our silhouette score for one cat. Then, we can repeat this for each cat and average the score for all cats to get the overall silhouette score. Silhouette score ranges from -1 to +1, and the higher the score, the better! A high score indicates that the cats are generally similar to the other cats in their clusters and distinct from the cats in other clusters. A score of 0 means that clusters are overlapping. So, if it turns out that the cats were sitting in distinct groups and your friend is good at clustering, we’d expect a high silhouette score.

Now, to use it in a sentence!

Serious: I am unsure of how many clusters I should group my data into for k-means clustering… it seems like choosing 3 or 4 will give me the same silhouette score of 0.38!

Less serious (suggested to me by ChatGPT): I tried sorting my sock drawer by color, But it’s a bit tricky with all those shades of grey. I mean, I can’t even tell the difference between dark grey and mid grey. My sock drawer’s silhouette score is so low!

See you in the blogosphere!
Lucie Yang

Imagine you have a photo of a cat sitting in a garden. If you want to describe the cat to someone who has never seen it, you might say it has pointy ears, a furry body, and green eyes. These details are the features that make the cat unique and distinguishable.

Similarly, in medical imaging, ML algorithms like CNN are widely used to analyze images like X-rays or MRIs. The CNN works like a set of filters that look for specific features in the image, such as edges, corners, or textures, and then combines these features to create a representation of the image.

For example, when looking at a chest X-ray, a CNN can detect features like the shape of the lungs, blood vessels, and other structures. By analyzing these features, CNN can identify patterns that indicate the presence of a disease like pneumonia or lung cancer. The CNN can also analyze other medical images, like MRIs, to detect tumors, blood clots, or other abnormalities.

To perform feature extraction, CNN applies a series of convolutional filters to the image, each designed to detect a specific pattern or feature. The filters slide over the image, computing the dot product between the filter and the corresponding pixel values in the image to produce a new feature map. These feature maps are then passed through non-linear activation functions to increase the discriminative power of the network. CNN then down-samples the feature map to increase the robustness of the network to translation and rotation. This process is repeated multiple times in a CNN, with each layer learning more complex features based on the previous layers. The final output of the network is a set of high-level features that can be used to classify or diagnose medical conditions.

Now let’s use feature extraction in a sentence!

Serious: “How can we ensure that the features extracted by a model are truly representative of the underlying data and not biased towards certain characteristics or attributes?”

Less Serious:
My sister: “You know, finding the right filter for my selfie is like performing feature extraction on my face.”

Me: “I guess you’re just trying to extract the most Instagram-worthy features right?”

From looking at the image from two different domains, could you tell what are they?
Hmmm? Is this a trick question or not, aren’t they the same? You might ask.
Yes, you are right. They are all bags. They are generally the same object, and I am sure you can easily tell just at a glimpse. However, unlike human beings, if you let a machine learning model read these images from two different domains, it would easily get confused by them, and eventually, make mistakes in identifying them. This is known as domain shift in Machine Learning.

Domain shift, also known as distribution shift, usually occurs in deep learning models
when the data distribution changes when the model reads the data. For instance, let’s say a deep learning model is trained on a dataset containing the images of backpacks on domain 1 (see the backpack image above). The model itself would then learn the specific features of the backpack image from domain 1 like the size, shape, angle of the picture taken etc. When you take the exact same model to test or retrain on the backpack images from domain 2, due to a slight variation in the background angle, the data distribution of the model encounters shifts a little bit, which would most likely result in a drop in model performance.

Deep learning models, such as a CNN model, are also widely used in the medical
imaging industry. Researchers have been implementing deep learning models in image
classification, segmentation and other tasks. However, because different imaging centers might use different machines, tools, and protocols, the datasets on the exact same image modality across different imaging centers might differ. Therefore, a model might experience a domain shift when it encounters a new unseen dataset which has variation in the data distribution.

Serious:
Me: “What can we do if a domain shift exists in a model between the source and target dataset?”
Professor Tyrrell: “Try mixing the target dataset with some images from the source dataset! ”

Less serious:
Mom: “I heard that your brother is really good at physics, what is your domain?”
Me: “I used to be an expert on Philosophy, but now due to my emerging interest in AI, I shift my domain to learning Artificial Intelligence.”
Mom: “Oh! A domain shift!”

Having just finished my intro to psychology course, I found that a useful way to learn the material (and guarantee a higher score on the test) was giving myself pop quizzes. In particular, I would write out a phrase and erase a keyword, then I will try to fill in the blank. Turns out this is such an amazing study method that even machines are using it! This method of learning, where the learner learns more in-depth by creating a quiz (e.g. fill-in-the-blank) for itself constitutes the essence of self-supervised learning.

Many machine learning models follow the encoder-decoder architecture, where an encoder network first extracts useful representations from the input data and the decoder network then uses the extracted representations to perform some task (e.g. image classification, semantic segmentation). In a typical supervised learning setting, when there is a large amount of data but only little of which is labelled, all the unlabelled data would have to be discarded as supervised learning requires a model be trained using input-label pairs. On the other hand, self-supervised learning utilizes the unlabelled data by introducing a pretext task to first pretrain the encoder such that it extracts richer and more useful representations. The weights of the pretrained encoder can then be transferred to another model, where it is fine-tuned using the labelled data to perform a specified downstream task (e.g. image classification, semantic segmentation). The general idea of this process is that better representations can be learned through mass unlabelled data, which provides the decoder with a better starting point and ultimately improves the model’s performance on the downstream task.

The choice of pretext task is paramount for pretraining the encoder as it decides what kind of representations can be extracted. One powerful pretrain method that has yielded higher downstream performance on image classification tasks is SimCLR. In the SimCLR framework, a batch of  images are first sampled, and each image is applied two different augmentations  and , resulting in  images. Two augmented versions of the same image is called a positive pair, and two augmented versions of different images is called a negative pair. Each pair of the  images is passed to the encoder  to produce representations  and , and these are then passed to a projection layer  to obtain the final representations  and . A contrastive loss defined using cosine similarity operates on the final representations such that the encoder  would produce similar representations for positive pairs and dissimilar representations for negative pairs. After pretraining, the weights of the encoder  could then be transferred to a downstream image classification model.

Although better representations may be extracted by the encoder using self-supervised learning, it does require a large unlabelled dataset (typically >100k images for vision-related tasks).

Now, using self-supervised learning in a sentence:

Serious: Self-supervised learning methods such as SimCLR has shown to improve downstream image classification task performance.

Less Serious: I thought you will be implementing a self-supervised learning pipeline for this project, why are you teaching the machine how to solve a rubik’s cube instead? (see Self-supervised Feature Learning for 3D Medical Images by Playing a Rubik’s Cube)

See you in the blogosphere!

Paul Tang