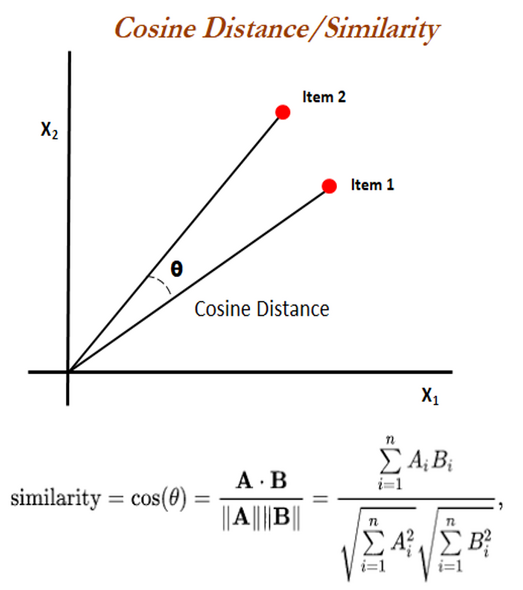
Today we will talk about a way to measure distance, but not about how far away two objects are. Instead, cosine distance, or cosine similarity, is a measure of how similar two non-zero vectors are in terms of orientation, or to put it simply, the direction to which they point. Mathematically, the cosine similarity between two 2-D vectors is equal to the cosine of the angle between them, which can also be calculated using their dot product and magnitudes, as shown on the right. Two vectors pointing in the same direction will have a cosine similarity of 1; two vectors perpendicular to each other will have a similarity of 0; two vectors pointing in opposite direction will have a similarity of -1. Cosine distance is equal to (1 – cosine similarity). In this case, two vectors will have a cosine distance between 0 to 2: 0 when they are pointing in the same direction, and 2 when they are pointing in opposite direction. Cosine similarity and distance essentially measure the same thing, but the distance will convert any negative values to positive.
Cosine distance and similarity also apply to higher dimensions, which makes them useful in analyzing images, texts, and other forms of data. In machine learning, we can use an algorithm to process a dataset of information and store each object as an array of multidimensional vectors, where each vector represents a feature. Then, we can use cosine similarity to compare how similar each pair of vectors are between the two objects and come up with an overall similarity score. In this case, two identical objects will have a similarity score of 1. In higher dimensions, we can rely on the computer to do the calculations for us. For example, we have the distance.cosine function in the SciPy package in Python will compute the cosine distance between two vector arrays in one go.
Here are two examples of how you can use cosine distance in a conversation:
Serious: “I copied an entire essay for my assignment and this online plagiarizing checker says my similarity score is only 1! Time to hand it in.” “It says a COSINE similarity of 1. Please go back and write it yourself…”
Less serious: *during a police car chase* “Check how far are we from the suspect’s car!” “Well, assuming that he doesn’t turn, the distance between us will always be zero. Remember from your math class? Two vectors pointing in the same direction will always have a cosine distance of zero…”
… I’ll see you in the blogosphere.
Jenny Du